こんにちは!アイデミーのSeiya_Takanoです。今回のブログでは、深層学習によって私の母が個人経営するスナックの売り上げを予測した結果をレポートします。
経営者である母は「在庫管理、雇用人数、設備投資、経営拡大」などの支出に関する判断にいつも悩まされています。そこで私は、確度の高い売り上げ予測ができれば、その苦労を少しでも減らせるかもしれないと思いました。
機械学習の勉強を始めて早1ヶ月が経ち、ちょうど、実際のデータでモデル構築してみたいなと思い始めたところでした。やり遂げられるか少し不安でしたが、これまでの復習も兼ねながら挑戦した結果をお伝えしたいと思います!!!また、これから機械学習を勉強する人への参考にもなれば良いなと思っています。
時系列データ解析について
「スナックの売り上げ予測のモデル構築」は、時系列データ解析に該当します。時系列データとは、時間の経過と共に変化するデータのことを指します。時系列データ解析は、会社の売り上げや商品の売り上げの予測にも応用できるので、ビジネスシーンでも非常に重要な分析技術とされています。
今回は、その中でも深層学習の手法を応用したRNN(Recurrent Neural Network)とLSTM(Long-short-term-memory)というアルゴリズムの使用を検討していきます。実装の前に、それぞれ簡単に解説します。
RNN(Recurrent Neural Network)
RNNとは、深層学習によって時系列データを解析する機械学習アルゴリズムの一つです。中間層において、前の時点のデータを現時点の入力として自己ループすることがRNNの特徴です。
これによってRNNでは、中間層におけるデータ同士の前後の文脈を保持したまま、情報の伝達が可能になります。そしてこの性質が、時間の概念を持つデータの学習を可能にしました。
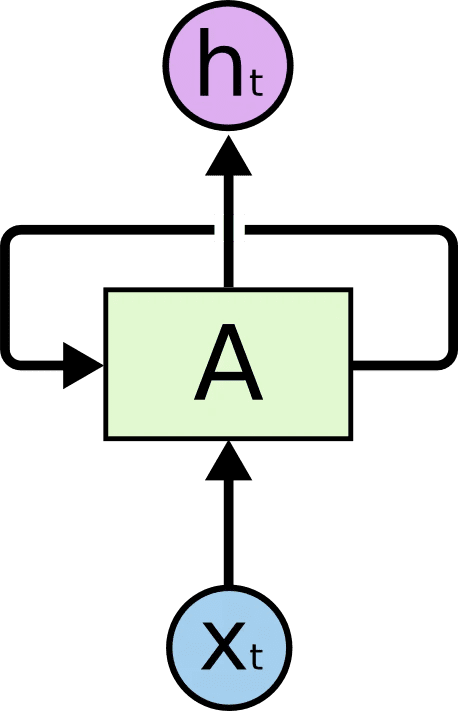
(http://colah.github.io/posts/2015-08-Understanding-LSTMs/より引用)
RNNの欠点
深層学習で時系列データの解析を可能にしたRNNですが、実は性能がそれほど高くはありません。その原因はRNNのループ構造によって活性化関数が何度も乗算されることにあります。
時間の経過と共に、繰り返し活性化関数が乗算されることで、勾配の値が収束する勾配消失、もしくは、演算量が指数的に増加する勾配爆発が起きてしまうのです。その結果、適切なデータ処理が難しくなってしまいます。また、これらの理由から、長期間の時系列データの学習にはRNNは向いていないことが分かります。
この欠点を解決した深層学習モデルが、次に紹介するLSTM(Long-short-term-memory)です。
LSTM(Long-short-term-memory)
LSTMモデルでは、中間層のセルをLSTMブロックに置き換えることで、RNNの持つ「長期間の記憶を保持しながら学習できない」という欠点を克服しています。LETMブロックの基本的な構成は以下です。
- CEC:過去のデータを保存するユニット
- 入力ゲート:前のユニットの入力の重みを調整するゲート
- 出力ゲート:前のユニットの出力の重みを調整するゲート
- 忘却ゲート:過去の情報が入っているCECの中身をどの程度残すかを調整するゲート
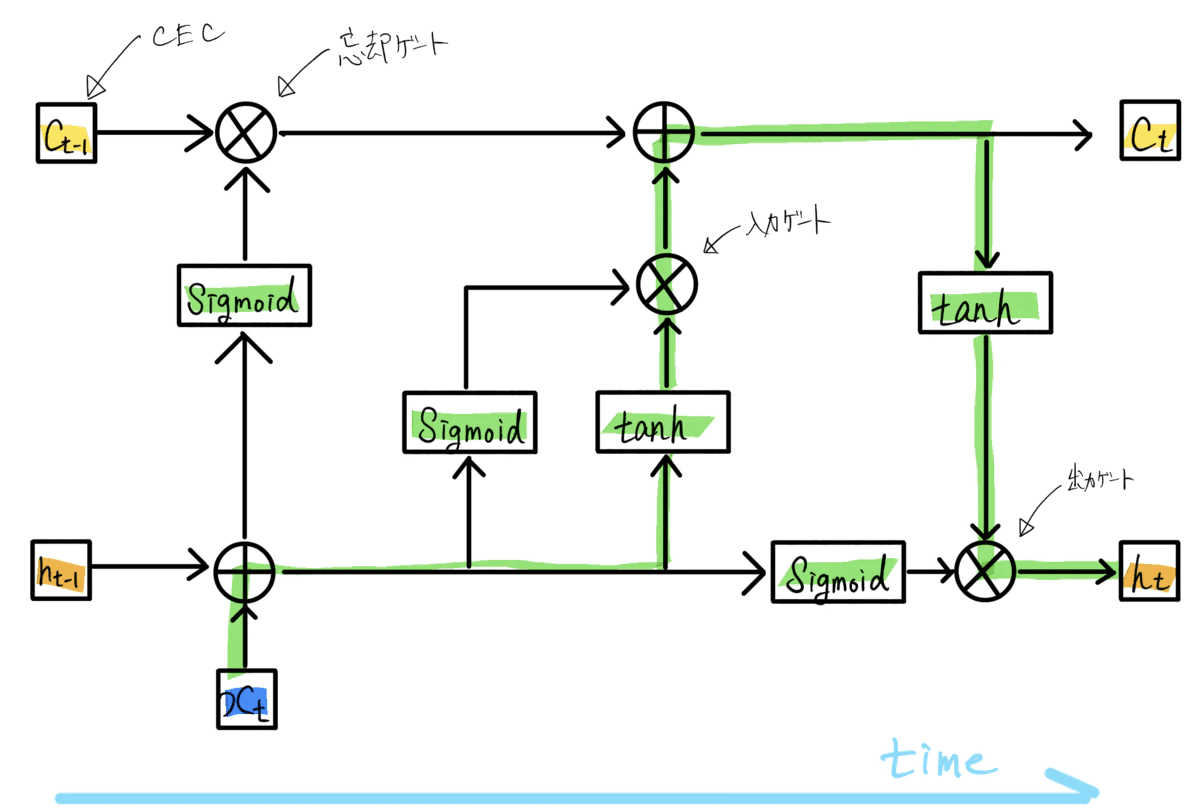
(https://sagantaf.hatenablog.com/entry/2019/06/04/225239より引用)
LSTMでは、上述したゲートの機能によって、セルの状態に応じた情報の削除・追加が可能です。入出力の重みを調整、セル内のデータの調整によって、RNNの欠点であった勾配消失と勾配爆発の問題を解消しています。よって、長期間の時系列データ解析にも適応することができます。
以上が、RNNとLSTMの理論的な説明になります。
今回取り扱うスナックの売り上げに関するデータは、7年分で計82データあります。長さとしては中長期間のデータなので、RNNとLSTM両方のモデルで予測し、結果の良いモデルを採用したいと思います。それでは実際にモデル構築をしていきます。
機械学習のモデル構築の流れ
機械学習のアルゴリズムの種類はたくさんありますが、根幹の部分にあるモデル構築の流れは全てにおいて共通しています。
機械学習の簡単な流れは以下の通りです。今回も、この流れを意識しながらモデル構築していきます。
- データ収集
- データの前処理(重複や欠損データ等を取り除いて、データの精度を高める)
- 機械学習の手法でデータを学習
- テストデータで性能をテスト
開発環境
- OS: Windows10
- python環境: Jupyter Notebook
ファイル構成
Forecast-
|-Forecast.py(pythonファイル)
|-sales_data-
|-各種CSVファイル
必要モジュール
まずは必要なモジュールをimportします。実行環境に以下のコードを書きます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import SimpleRNN
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
データ収集
まずはデータ収集です。渋る母を説得し、スナックの売り上げデータをゲットしました。月ごとの売り上げをまとめた2013~2019年のエクセルデータの形を整えてCSV形式に出力します。
収集データについて
データの説明
2013~2019年の月別のスナックの売り上げ記録。
基本統計量
sales
データ数 8.400000e+01
平均 7.692972e+05
標準偏差 1.001658e+05
最小値 5.382170e+05
1/4分位数 7.006952e+05
中央値 7.594070e+05
3/4分位数 8.311492e+05
最大値 1.035008e+06
年別の売り上げ平均
年が経過するごとに売り上げがアップしている傾向がありそうです。
2019 : 801197 円
2018 : 822819 円
2017 : 732294 円
2016 : 755799 円
2015 : 771255 円
2014 : 761587 円
2013 : 740128 円
月別の売り上げ平均
一番売り上げ額が多いのは12月、次に4月という結果になりました。年末の飲み会や年度初めの飲み会が多く開かれることが大きく関わっていそうです。こういった傾向もしっかり予測できたらと思います。
1 月: 758305 円
2 月: 701562 円
3 月: 750777 円
4 月: 805094 円
5 月: 785633 円
6 月: 778146 円
7 月: 752226 円
8 月: 763773 円
9 月: 689561 円
10 月: 765723 円
11 月: 779661 円
12 月: 901100 円
時系列の周期変動とトレンドの考察
トレンドとは?
データの長期的な傾向を意味します。今回のテーマでは、長期的にスナックの売り上げが増加しているのか、それとも減少しているのかを示します。
周期変動とは?
周期変動があるデータは、時間の経過に伴ってデータの値が上昇と下降を繰り返します。特に1年間での周期変動を季節変動と言います。今回のテーマに関しては、先ほどの考察で飲み会が多くなる12月と4月の売り上げの平均額が高いことが分かりました。おそらく季節的な周期変動がありそうですね。
fig = sm.tsa.seasonal_decompose(df_sales_concat, freq=12).plot()
plt.show()

予想通り、売り上げに関する増加トレンドがありました。また、4月と12月に売り上げが多くなるという周期変動もありました。こういった内容に関しても、機械学習モデルで予測できたら良さそうですね。
時系列の自己共分散
時系列の自己共分散とは、同じ時系列データの別々の時点同士での共分散を指します。k次の自己共分散とは、k時点離れたデータとの共分散を指します。この自己共分散をkの関数として見たものを自己相関関数といいます。この関数をグラフで表したものをコレログラムといいます。
df_sales_concat_acf = sm.tsa.stattools.acf(df_sales_concat, nlags=12)
print(df_sales_concat_acf)
sm.graphics.tsa.plot_acf(df_sales_concat, lags=12)
fig = sm.graphics.tsa.plot_acf(df_sales_concat, lags=12)
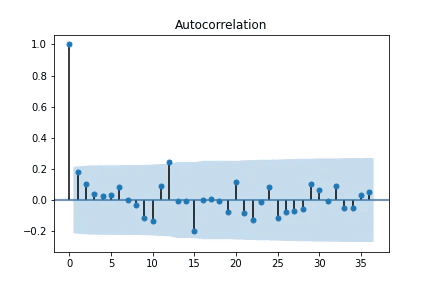
コレログラムから、k=12の時に自己相関係数が高くなることが分かります。月別の売り上げを記録したデータなので、あるデータとその1年前のデータとの間に相関関係があることが分かります。
df_2019 = pd.read_csv('./sales_data/2019_sales.csv')
df_2018 = pd.read_csv('./sales_data/2018_sales.csv')
df_2017 = pd.read_csv('./sales_data/2017_sales.csv')
df_2016 = pd.read_csv('./sales_data/2016_sales.csv')
df_2015 = pd.read_csv('./sales_data/2015_sales.csv')
df_2014 = pd.read_csv('./sales_data/2014_sales.csv')
df_2013 = pd.read_csv('./sales_data/2013_sales.csv')
df_sales_concat = pd.concat([df_2013, df_2014, df_2015,df_2016,df_2017,df_2018,df_2019], axis=0)
index = pd.date_range("2013-01", "2019-12-31", freq='M')
df_sales_concat.index = index
del df_sales_concat['month']
dataset = df_sales_concat.values
dataset = dataset.astype('float32')
データの前処理(データセットの作成)
次にデータの前処理です。具体的にはモデル構築に使用するデータセットを作成していきます。
Forecast.py
train_size = int(len(dataset) * 0.67)
train, test = dataset[0:train_size, :], dataset[train_size:len(dataset), :]
scaler = MinMaxScaler(feature_range=(0, 1))
scaler_train = scaler.fit(train)
train_scale = scaler_train.transform(train)
test_scale = scaler_train.transform(test)
look_back =1
train_X, train_Y = create_dataset(train_scale, look_back)
test_X, test_Y = create_dataset(test_scale, look_back)
train_X_original, train_Y_original = create_dataset(train, look_back)
test_X_original, test_Y_original = create_dataset(test, look_back)
train_X = train_X.reshape(train_X.shape[0], train_X.shape[1], 1)
test_X = test_X.reshape(test_X.shape[0], test_X.shape[1], 1)
RNNモデルとLSTMモデルの構築と学習
RNNモデル構築
Forecast.py
rnn_model = Sequential()
rnn_model.add(SimpleRNN(64, return_sequences=True, input_shape=(look_back, 1)))
rnn_model.add(SimpleRNN(32))
rnn_model.add(Dense(1))
rnn_model.compile(loss='mean_squared_error', optimizer='adam')
rnn_model.fit(train_X, train_Y, epochs=100, batch_size=64, verbose=2)
LSTMモデル構築
Forecast.py
lstm_model = Sequential()
lstm_model.add(LSTM(64, return_sequences=True, input_shape=(look_back, 1)))
lstm_model.add(LSTM(32))
lstm_model.add(Dense(1))
lstm_model.compile(loss='mean_squared_error', optimizer='adam')
lstm_model.fit(train_X, train_Y, epochs=100, batch_size=64, verbose=2)
以上で、データセットからRNNとLSTMによる機械学習が完了しました。使用するクラスが異なるだけで、基本的な操作はどちらも同じです。
次に結果をグラフにプロットするための処理です。ここからはモデルをmodelと表示しますが、lstm_modelとrnn_modelの2つを指します。
Forecast.py
train_predict = model.predict(train_X)
test_predict = model.predict(test_X)
train_predict = scaler_train.inverse_transform(train_predict)
train_Y = scaler_train.inverse_transform([train_Y])
test_predict = scaler_train.inverse_transform(test_predict)
test_Y = scaler_train.inverse_transform([test_Y])
train_score = math.sqrt(mean_squared_error(train_Y_original, train_predict[:, 0]))
print(train_score)
print('Train Score: %.2f RMSE' % (train_score))
test_score = math.sqrt(mean_squared_error(test_Y_original, test_predict[:, 0]))
print('Test Score: %.2f RMSE' % (test_score))
train_predict_plot = np.empty_like(dataset)
train_predict_plot[:, :] = np.nan
train_predict_plot[look_back:len(train_predict)+look_back, :] = train_predict
train_predict_plot = pd.DataFrame({'sales':list(train_predict_plot.reshape(train_predict_plot.shape[0],))})
train_predict_plot.index = index
test_predict_plot = np.empty_like(dataset)
test_predict_plot[:, :] = np.nan
test_predict_plot[len(train_predict)+(look_back*2):len(dataset), :] = test_predict
test_predict_plot = pd.DataFrame({'sales':list(test_predict_plot.reshape(test_predict_plot.shape[0],))})
test_predict_plot.index = index
次は実際のデータをグラフにプロットしていきます。
Forecast.py
plt.title("monthly-sales")
plt.xlabel("time(month)")
plt.ylabel("sales")
plt.plot(dataset, label='sales_dataset', c='green')
plt.plot(train_predict_plot, label='train_data', c='red')
plt.plot(test_predict_plot, label='test_data', c='blue')
plt.yticks([500000, 600000, 700000, 800000, 900000, 1000000, 1100000])
plt.legend()
plt.show()
結果
結果として出力されたRNNとLSTMのグラフをそれぞれ掲載します。
RNNによる予測
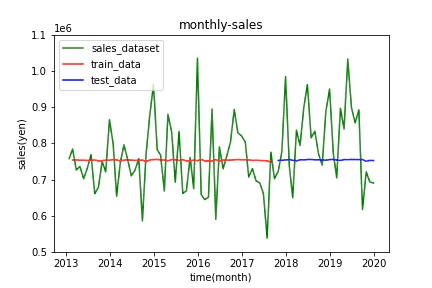
出力の値が完全に消失しています。パラメータをいろいろ変えましたが、結果に大きな変化はありませんでした。今回の84データの時間の長さでもRNNでの手法は向いていないことが分かります。
LSTMによる予測
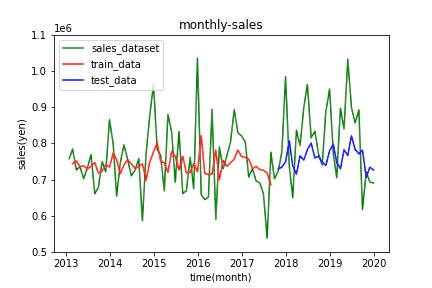
RNNによる予測に比べると、売り上げの傾向をなんとなく予測できています。特に4月と12月で売り上げが増加する傾向をおさえることができています。
しかし全体として、実測値と大きく外れている点が多く見受けられます。モデルの良さの基準になるRMSEに関してもTrain Score: 94750.73 RMSE, Test Score: 115472.92 RMSEとなり、かなり大きい値になっています。あまり良い結果とは言えなそうです。
まとめ
RNNで勾配消失を起こすデータセットでも、LSTMで詳しい時系列解析が実現できることがわかりました。しかし、LSTMでの予測でも売り上げの傾向を示すだけにとどまり、実際の値から大きく外れた値が多く見受けられます。これでは、確度の高い売り上げ予測とは言えず、経営判断の根拠となる収入データの予測にはなりえません。
考察
RNN、LSTMどちらに関しても、パラメータであるloop_back, epochs, batch_sizeのいろいろなパターンを試しましたが、特に性能が上がることはありませんでした。
原因としては、データの少なさとばらつきが想定できます。後に調べたところ、時系列解析でのデータ数84はかなり少ない数だそうです。機械学習モデルの構築には、データが命であるということを身にしみて感じました。
しかし、何はともあれ、1か月の機械学習の復習と初学者への良い教材にはなったかと思います。これから機械学習エンジニアとしてレベルアップできるように、さらに精進していきます!
▼この記事はQiitaでも公開しています。
https://qiita.com/Seiya_Takano/items/eb8d26c66e388f3afc3a








