こんにちは。Aidemy研修生の藤川です。 機械学習というと何かを予測するということを考える人が多いのではないでしょうか。 株やFX、仮想通貨の価格を予想しているブログも多々ありますが、金の価格はどうでしょうか。

なぜ金か? というと、以下のリンクにある通り、金の価格予想自体は昔からされています。 jpyforecast.com
しかし、機械学習を使った予測はどうやらあまり行われていないようです。 ということで、この価格予想に負けじと、機械学習を用いて予測を行ってみたいと思います! 今回はGoogle Colaboratoryを使用しています。 もし使用する場合は、ランタイムの変更でGPUを指定しておくことを忘れないようにしてください。 実行環境(lshwを使用して確認)
OS : ubuntu17.10
CPU : Intel(R) Xeon(R) CPU @ 2.20GHz
GPU : Tesla K80
メモリ : 12GB
このようにある程度のスペックの環境であることがわかります。 自分のPCのスペックが足りない場合には非常に役立ちそうですね。 import部分はこのようになっています。
import pandas as pd
import numpy as np
import io
from google.colab import files
import matplotlib.pyplot as plt
import statsmodels.api as sm
from datetime import datetime
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.arima_model import ARIMA
import warnings
import itertools
%matplotlib inline
データの取得
まず、金の価格のデータを取得しなければいけません。 データは以下のサイトから取得できます。 lets-gold.net 今回は2016年と2017年のデータをもとに学習を進めていきます。 データの読み込みを行います。時系列解析では連続した日付のデータが求められますが、 金の価格は土日・祝日に更新がされないので日付を適当につけなおしてあげます。
#ファイルをアップロードする
uploaded = files.upload()
#アップロードされたファイルを読み込む
gold_data = pd.read_csv("historical_data_2016.csv")
gold_data2 = pd.read_csv("historical_data_2017.csv")
#必要のない列は削除しておく。
gold_ = gold_data.drop(columns = ["DATE","PT_TOKYO","GOLD_NY","PT_NY","USDJPY"])
gold_.dropna()
gold2_ = gold_data2.drop(columns = ["DATE","PT_TOKYO","GOLD_NY","PT_NY","USDJPY"])
#データの結合
gold = pd.concat([gold_,gold2_])
#ここで日付を付け直してあげる
gold.index = pd.date_range("2016-01-01","2017-05-06",freq = "D")
データの関係を調べる
ここで、データの関係を確認することにします。 このブログを参考に進めていきます。 www.kumilog.net まずは、自己相関係数を求めます。 簡単に言うと、自己相関係数を調べることで何個前のデータが大きな影響を及ぼしているかがわかります。
fig=plt.figure(figsize=(12,8))
ax = fig.add_subplot()
#自己相関係数
sm.graphics.tsa.plot_acf(gold_data["GOLD_TOKYO"], lags=80,ax = ax)
plt.show()
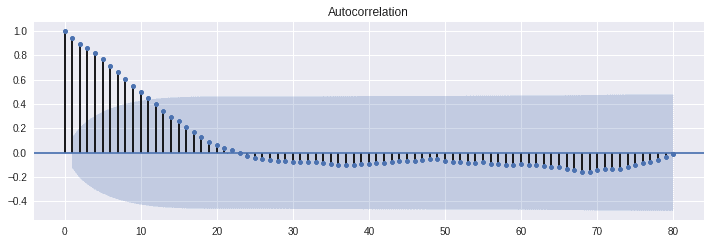
ここで、色が濃くなっているところが95%信頼区間です。 だいたい10個前までのデータに大きく影響を受けていることがわかります。 次に偏自己相関係数を求めます。
fig=plt.figure(figsize=(12,8))
ax = fig.add_subplot(212) #偏自己相関係数 fig = sm.graphics.tsa.plot_pacf(gold_data["GOLD_TOKYO"], lags=80, ax=ax) plt.show()
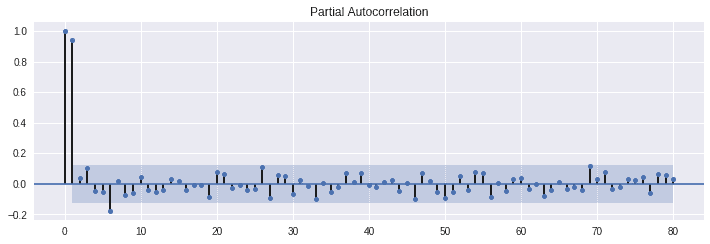
偏自己相関係数では、ある点とある点の間の関係をダイレクトに調べることが出来ます。 例えば、今日と2日前のデータの関係を調べる時、1日前のデータの影響も受けますが、 偏自己相関係数を用いると1日前の影響を取り除いて考えることが出来ます。
この結果を見る限り、前日の影響を大きく受けることがわかります。 また、6日目もある程度大きな影響を与えていることもわかります。 69日目は95%信頼区間をギリギリ超えています。ここも何か関係がある可能性がありますね。
最後に、ADF検定を行います。 ADF検定では単位根過程でないかどうかを判定できます。 詳しくは以下の記事をご覧ください。
logics-of-blue.com pythonではstatsmodelsで簡単にADF検定を行うことが出来ます。
adf_result = sm.tsa.stattools.adfuller(gold_data["GOLD_TOKYO"],autolag='AIC')
adf = pd.Series(adf_result[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
print(adf)
結果は以下のようになります。
Test Statistic -3.089297
p-value 0.027355
#Lags Used 5.000000
Number of Observations Used 239.000000
p値は0.027355と、 p < 0.05であるので単位根過程ではないことがわかります。 単位根過程ではないということでここから安心して学習を進めていきます。
モデルの決定・学習
今回は時系列のデータなので、1番基礎となるSARIMAモデルを使用します。 SARIMAモデルについてはこちらのサイトでよく理解できると思います。 deepage.net 学習部分についてはこのようにスマートにかくことが出来ます。
N = 420
test = gold[:]
gold = gold[:N]
SARIMA_gold = sm.tsa.statespace.SARIMAX(gold,order=(1,0,1),seasonal_order = (1,1,1,69), enforce_stationarity = False, enforce_invertibility = False,trend = "n").fit(trend='nc',disp=False)
print(SARIMA_gold.summary())
pred = SARIMA_gold.predict()
pred2 = SARIMA_gold.forecast()
自己相関係数より、q = 1 偏自己相関係数より p = 1
gold_diff = gold_.diff()
gold_diff.index = gold_data.index
gold_diff = gold_diff.dropna()
また、季節成分はありませんが、1回階差の季節成分を抽出し、グラフを参照します。
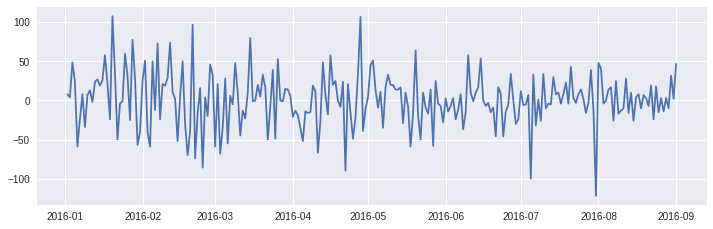
また、移動平均を青色で表示します。 sin波とならべてみると、微妙に季節性を感じます。
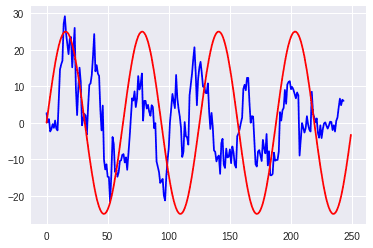
グラフをよく見ると3ヶ月ごとの周期を感じるので、周期s = 69を決定しました。 以上よりSARIMA(1,0,1)(1,1,1,69)を決定しました。 モデルの学習結果はこのようになります。

AIC,BICともに2000超えという非常に残念な結果となっています。 一般に、AIC、BICは小さい方が良いモデルとされる傾向があります。 AIC,BICについては以下の記事に詳しく説明があります。 www.atmarkit.co.jp 一応、データをプロットしてみます。
plt.plot(gold_,color = "b")
plt.plot(gold2_,color = "b")
plt.plot(pred,color = "r")
plt.plot(pred2,color="y")
plt.xlim(["2016-05-01","2017-06-06"])
plt.ylim([4400,5200])
plt.show()
青が学習データ、赤が学習させた結果、そして黄色が予測です。
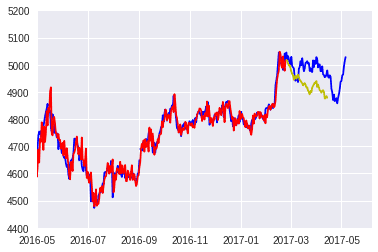
あまりグラフの形は似ていませんね、改善が必要なようです。 騰落も調べてみます
data_score = 0
for i in range(49):
if pred[i+1] - pred[i] > 0:
if test.values[N+1+i] - test.values[N+i] > 0:
data_score += 1
if pred[i+1] - pred[i] < 0:
if test.values[N+1+i] - test.values[N+i] < 0:
data_score += 1
print("正解率:" + str(100*data_score/50) + "%")
正解率は50%となり、ランダムウォークですね…といった結果です…
モデルの精度を上げる
標準化を行います。 標準化を行うので、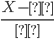 データをに従わせます。
データをに従わせます。
gold_mean = np.mean(gold.values)
gold_std = np.std(gold.values)
gold_b = (gold - gold_mean)/gold_std
SARIMA_std = sm.tsa.statespace.SARIMAX(gold_b,order=(1, 0, 1),seasonal_order = (1,1,0,69), enforce_stationarity = False, enforce_invertibility = False,trend = "n").fit(trend=>'nc',disp=False)
print(SARIMA_std.summary())
pred_b = SARIMA_std.predict()
pred2_b = SARIMA_std.forecast()
モデルの結果です。

AICは4,BICは24まで落ちました!!! この数値は小さい方が良いので標準化が非常に効果的であることが確認できました。 グラフを表示します。
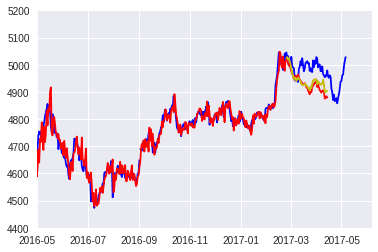
赤が標準化する前の予測で、黄色が標準化したあとの予測です。 グラフの形はあまりフィットしていませんね。もう少しうまくいくといいのですが・・・ 騰落の正解率は54%!!!!!!!! 少しだけ精度が上がっているようです。
ランダムウオークの実装
実際の金の価格もランダムウォークとなっています。 こちらの記事を参考にランダムウォークをSARIMAモデルで実装してみます。 stats.stackexchange.com SARIMA(0,1,0)(1,1,1,69)としてみます
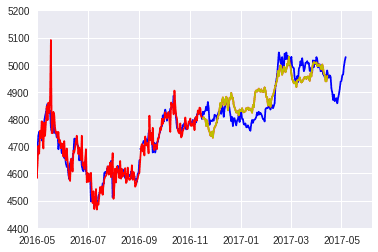
比較的フィットするグラフを描くことができました。 Introduction to ARIMA models こちらの記事を参考にすると、ARIMA(0,1,0)はAR(1)過程に従うようです。 d.hatena.ne.jp たしかに今回のデータも自己相関係数がこちらの記事の通りの形となっています。
番外編
ランダムフォレストで学習を進めてみました。 今回は、4日前までの価格をもとに学習を進めています。
gold["lag1"] = gold["GOLD_TOKYO"].shift(1)
gold["lag2"] = gold["GOLD_TOKYO"].shift(2)
gold["lag3"] = gold["GOLD_TOKYO"].shift(3)
gold["lag4"] = gold["GOLD_TOKYO"].shift(4)
gold.dropna()
N = 420
X_train = np.delete(gold[['lag1', 'lag2', 'lag3']][:N].values,[0,1,2],0)
X_test = np.delete(gold[['lag1','lag2','lag3']][N:].values,[0,1,2],0)
y_train = np.delete(gold['GOLD_TOKYO'][:N].values,[0,1,2],0)
y_test = np.delete(gold['GOLD_TOKYO'][N:].values,[0,1,2],0)
from sklearn.ensemble import RandomForestRegressor
r_forest = RandomForestRegressor(
n_estimators=100,
criterion='mse',
random_state=1,
n_jobs=-1
)
r_forest.fit(X_train, y_train)
y_train_pred = r_forest.predict(X_train)
y_test_pred = r_forest.predict(X_test)
結果は、、、

赤が元データ、黄色が予測です。 めちゃくちゃフィットしてる…!!!! …騰落の正解率は26.25%… 上下動の精度は落ちるがグラフにはフィットしています。
まとめ
ランダムウォークについてですが、こちらのブログを参考に考えてみます。 omedstu.jimdo.com たしかに、金の価格は前日の影響を非常に大きく受けるため、AR(1)過程が最もフィットするというのも納得です。 これは金だけでなく、株やFX、仮想通貨でも同様にAR(1)過程での予測も効果的なのではないでしょうか。
ただ、実際株やFX、仮想通貨、金などの予測は単一の手法では十分な予測精度が得られないと思います。 いくつかのモデルを構築し、総合的な判断をすることが必要となります。 正解率を中心に結果を見ていますが、実際に金の投資として考えた時、長期的にどれほど上昇するかが大事になります。
つまり、ランダムフォレストのような形式で長期の見立てをつけ、SARIMAモデルなどで上昇の信ぴょう性を見ていくことがもっとも良いのではないでしょうか。 今回は手軽に行えるSARIMAモデル、ランダムフォレストを紹介しましたが、 先日のブログのようにLSTMを使用した方が良い結果が得られると思います。 前処理としてFFTでローパスフィルタをかける方法も金融工学では一般的なようです。
blog.aidemy.net こちらのブログを参考に、是非LSTMも実装してみてください。







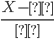 データをに従わせます。
データをに従わせます。





