昨今、「機械学習」というワードをよく耳にするかと思います。 その機械学習の種類は大きく3つに分類されます。
- 教師あり学習
- 教師なし学習
- 強化学習
このブログでは教師あり学習に焦点を絞ります。
教師あり学習って何?
簡単にいうと、教師あり学習は人間の真似ができるようにするコンピュータの技術です。私たちも、先生のいうことを聞いて学習していましたよね。つまり、「教師あり学習」という概念は機械学習に限らず、人間の学習にも適用されるのです。
教師あり学習は大体、分類問題と回帰問題に分けられます。「分類問題」とは、あるデータをそれぞれカテゴリに分類することを言います。他者から送られてきたメールがスパムメールに勝手に分類されることがありますよね。これも、機械がメールをスパムメールか、非スパムメールかを分類した結果なのです。回帰問題はまた別の機会に扱うとして、今回は詳しく分類問題について見て行きましょう。
分類問題
分類問題を解くアルゴリズムは様々なものがあります。その全容については以下を参考してください。 qiita.com 教師あり学習の場合、学習データとテストデータをあらかじめ用意し、それらを用いて分類問題を解くわけですが、学習データを構成する個々の特徴は、測定単位の取り方で大きな値になったり小さな値になったりするので、分布の形状もそれに伴って大きく変化します。
よって、最適な性能を得るために特徴量のスケーリングが必要になってくるわけです。ここでは、測定単位の影響を取り除く一つの方法、個々の特徴を平均0、分散1にする「標準化」という手法について説明します。
標準化
標準化とは、以下の数式を用いて元のデータと標準偏差を用いて線形変換することを言います。
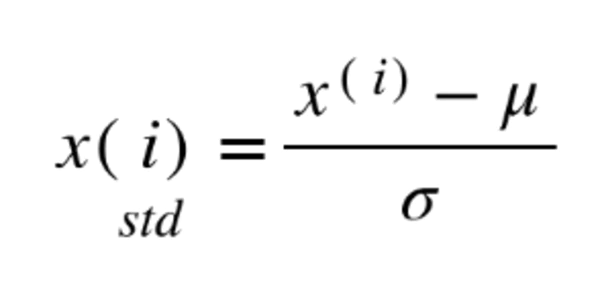
μ:元データの平均 σ:元データの標準偏差
特徴ごとに標準化を行うことで、測定単位の影響がない特徴ベクトルを構成することができます。
アヤメデータを用いた標準化
scikit-learnにもあるアヤメデータ(iris)は、3種のアヤメ(setosa,versicolor,virginica)それぞれ50個の花弁と萼の長さと幅からなる4次元データであり、統計の分野でベンチマークとして利用されています。4次元データは視覚化できないので、3種のアヤメの間で分離が良い花弁の長さと幅を用いて標準化の例を示します。それらの散布図をFig1、コードを以下に示します。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
df_iris = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data",header=None)
df_iris.columns = ["sepal length","sepal width","petal length","petal width","class"]
X = df_iris.loc[:,['petal length','petal width']]
y = df_iris.iloc[:,4]
sc.fit(X)
X_std = sc.transform(X)
plt.figure(figsize=(10,10))
plt.scatter(X.iloc[:50,0],X.iloc[:50,1],color='red',label="Setosa")
plt.scatter(X.iloc[50:100,0],X.iloc[50:100,1],color='blue',label="Versicolour")
plt.scatter(X.iloc[100:150,0],X.iloc[100:150,1],color='green',label="Virginica")
plt.scatter(X_std[:50,0],X_std[:50,1],color='red',marker='x',label="Setosa[Standardized]")
plt.scatter(X_std[50:100,0],X_std[50:100,1],color='blue',marker='x',label="Setosa[Standardized]")
plt.scatter(X_std[100:150,0],X_std[100:150,1],color='green',marker='x',label="Setosa[Standardized]")
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.legend(loc="lower right")
plt.xlabel("sepal length[cm]",fontsize=15)
plt.ylabel("sepal width[cm]",fontsize=15)
plt.title("Fig 1. Relationship between sepal length of sepal width",fontsize=20)
plt.xlim(-3,8)
plt.ylim(-2.0,3.0)
plt.grid(True)
plt.show()

Fig.1では、適切な線形変換が行われており楕円状に分布してるデータの中心が、標準化により原点に移動していることが確認できます。これを中心化といいます。また、データの広がりも各次元同じになります。ついでにこの標準化されたデータを分類問題に適用して見ます。分類機は単純パーセプトロンを使用しました。
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
sc.fit(X_train)
X_test_std = sc.transform(X_test)
X_train_std = sc.transform(X_train)
ppn.fit(X_train,y_train)
ppn1.fit(X_train_std,y_train)
y_pred = ppn.predict(X_test)
y_pred1 = ppn1.predict(X_test_std)
print ("Misclassified samples:%d"%(y_test != y_pred).sum())
print ("Misclassified samples[Standardized]:%d"%(y_test != y_pred1).sum())
print ("Accuracy:%.2f"%accuracy_score(y_test,y_pred))
print ("Accuracy[Standardized]:%.2f"%accuracy_score(y_test,y_pred1))

結果として、データを標準化によりスケーリングすることにより分類精度が31%向上することができました。以上の結果より標準化という手法が有効であることがわかります。今回は、標準化について解説しましたが、他にも無相関化、白色化などのスケーリング手法があります。
参考文献
執筆するにあたり参考にした書籍を以下に掲載いたします。
・ はじめてのパターン認識 平井有三 2017年3月10日 第1版第7刷

・ Python機械学習プログラミング 達人データサイエンティストによる理論と実践Sebastian Raschka 2016年10月11日 第1版第4刷
・ 人工知能はどのようにして「名人」を超えたのか? 山本一成 2017年7月12日 第4刷